
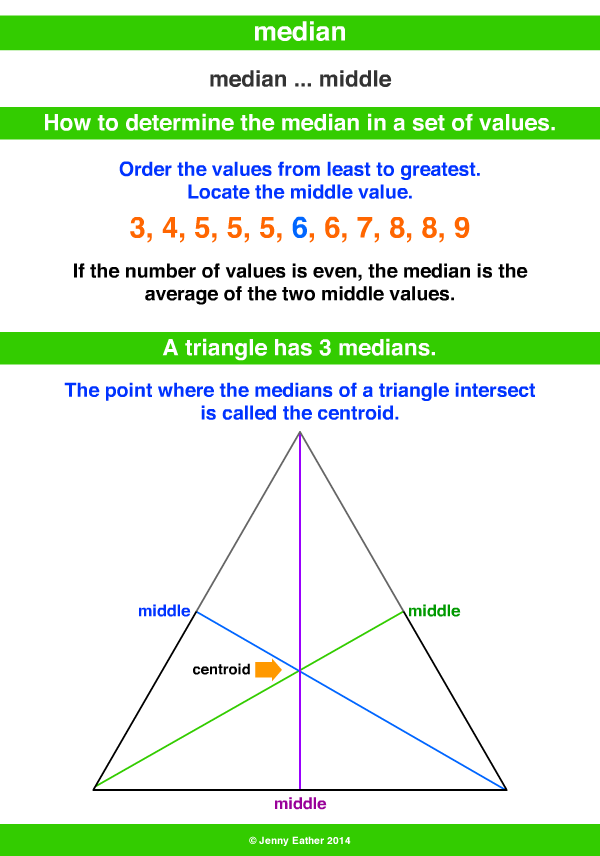
Math Education Geometry Problem 854: Triangle, Parallel lines.
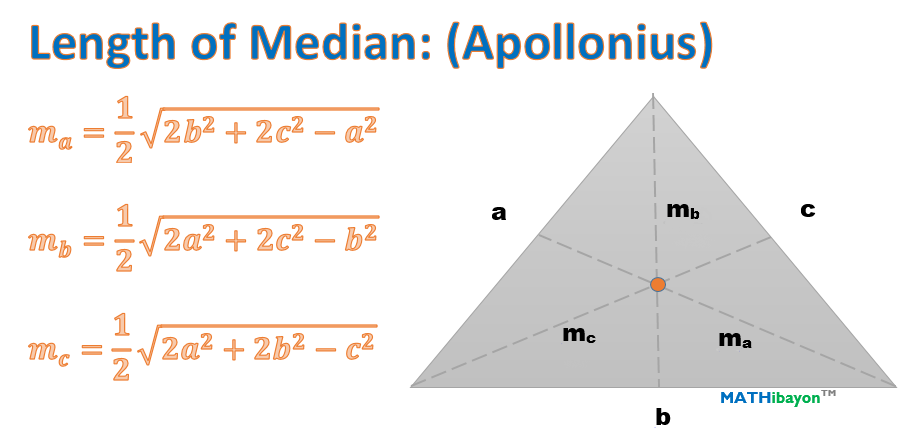
(Hint: Write AC and AM in termas of a, b and c.) Therefore AG and AM are parallel, so G lies on the line AM, as claimed. Median Length theorem Geometry Questions, Sat Prep, Theorems, Elearning, Maths, 2d. (Hint: How can you state the fact that M is the midpoint of BC in terms of vectors?) (b) Find a scalar k such that ACkAM. (a) Find (with proof) a formula for m in terms of b and c. You can check similarly that G lies on the other two medians, which proves that all three medians intersect at G. 3 In this problem, we will prove that G lies on the median AM. Let G be the point with position vector g=a(a + b + c). We will use similar notation for other points, i.e., b OB, cOC etc. In a triangle, median is a line segment joining a vertex to the midpoint of the corresponding opposite side. Let a be the position vector of A, that is, a-OA where denotes the origin. A theorem from plane geometry states that in any triangle, all three medians intersect in a single point G, the centroid of the triangle. 5.4 Medians and Altitudes A median of a triangle is a segment whose endpoints are a vertex and the midpoint of the opposite side. A median of a triangle is a line connecting a vertex of the triangle with the midpoint of the opposite side. In such a case, the median would still account for the very small outliers.Transcribed image text: 5. In such cases, the arithmetic mean would again, not be the best representation of the average value to use. In this particular case, even if there were very small outliers (say if 2 out of the 47 people actually earned only $5,000 a year), they would not significantly affect the result, but in different scenarios they could have a significant effect. In contrast, the median, since it is exactly in the middle of the values, isn't affected by either very large or very small values, and better represents the data since the median is what 94% of people in the room earn. This tutorial introduces you to the median of a triangle and shows you how many medians each triangle has Keywords: definition median median triangle. Clearly this is not a good representation of what the average person in the room earns. Since the median C G passes through points. If G is the midpoint of side A B of the given triangle, then its coordinates are given as ( 3 + 5 2, 2 + 4 2) ( 2 2, 6 2) ( 1, 3). Find the arithmetic mean of these two numbers to find the medianĮven though there are only three people who earn more than $55,000 in this example, and they comprise only 6% of the people in the room, because they earn vastly more, they skewed the mean income such that the value is almost 12 times more than what 94% of the people in the room earn. To find the equation of the median of a triangle we examine the following example: Consider the triangle having vertices A ( 3, 2), B ( 5, 4) and C ( 3, 8). The Shape class is a FrameworkElement and therefore participates in the layout system its derived classes can be used as the content of any element that supports UIElement children.
#MEDIAN GEOMETRY HOW TO#
How to quickly determine the number in the middle Note that it is possible that we could've gotten lucky and that 12 could've been in the middle of the first set of data, but we should not be trying to determine the median unless the data is listed in ascending or descending order.
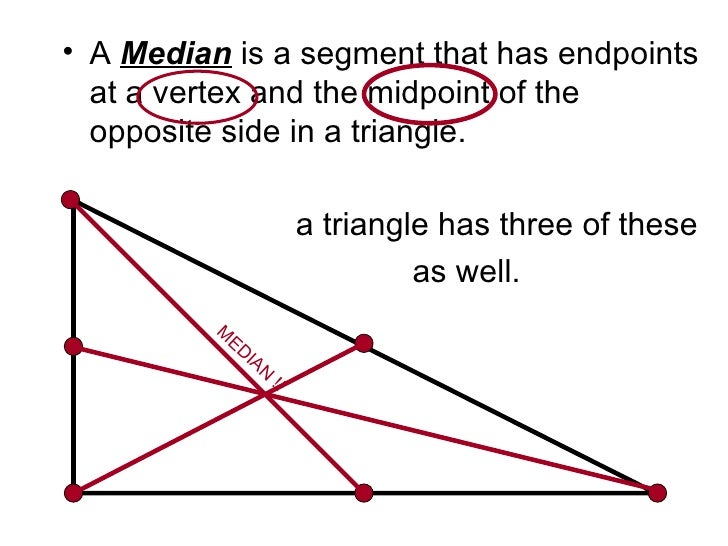
We need to first rearrange the numbers before attempting to determine the median. Now a median of the triangle- and well see a triangle has three of them- is just a line that connects a vertex of the triangle with the midpoint of the opposite side. Since there is an even number of values in the data set, we need to find the arithmetic mean of the two middle numbers, 5 and 4: The height or altitude of a triangle is a line segment drawn. 6 is the median, since it is the number in the middle.Ģ. A median is a line segment which joins a vertex of a triangle to the midpoint of the opposite side.


 0 kommentar(er)
0 kommentar(er)
